The Math Behind the Functions#

Investment tax-net value#

In general, an investment’s tax-net value can be calculated by

\[V_0 + (V_n - V_0)\,(1 - tr)\]

Where:

\(V_0\) is the initial value of the investment.
\(V_n\) is the final gross value of the investment.
\(n\) is the number of compounding periods (generally years).
\(tr\) is the tax rate applicable to that investment.

This can be simplified to

\[V_n\,(1-tr) + V_0\,tr\]

This applies for both the \(PPR\) and its \(Underlying \; Assets\). The only difference is the \(tr\) applied.

Investment gross value and PPR costs#

The gross final values, \(V_n\), for the PPR and its Underlying Assets (UA) can be calculated by

\[UA_n = V_0\,(1 + r)^n\]

and

\[PPR_n = UA_n\,(1 - cr_{PPR})^n = V_0\,(1 + r)^n\,(1 - cr_{PPR})^n\]

Where:

\(UA_n\) is the final gross value of an investment in the PPR’s UA.
\(PPR_n\) is the final gross value of an investment in a PPR, not considering any tax credit.
\(r\) is the UA’s cumulative annual growth rate (CAGR).
\(cr_{PPR}\) is the total PPR-specific cost incurred by the investor every year, expressed as a percentage of the year’s investment value. It includes the management commission, banking fees, audits, and other costs of running the fund.

PPR Tax Benefits#

Investment in a PPR generates a tax credit in the following year of \(20\%\) of the amount investment, until that amount reaches a certain limit depending on the investor’s age.

\[TC_0 = V_0 \, (tcp_{PPR})\]

Where:

\(TC_0\) is the tax credit.
\(tcp_{PPR}\) is the percentage of \(V_0\) returned as tax credit. We can consider it as always either \(0\) or \(20\%\), because even an investment that is not fully considered for the tax credit can be split between the portion that is considered in \(20\%\) and the portion that does not generate any tax credit.

If we assume that \(TC\) is invested in the PPR, we have

\[TC_n = TC_0\,(1+r)^n\,(1-mc)^n\]

Where:

\(TC_n\) is the final gross value of the investment of the tax credit in a PPR.
\(TC_0\) is the initial value of the tax credit.

PPR tax-net value#

Given the expressions above, we can get the tax-net value of an investment in a PPR as

\[V_0 + (PPR_n - V_0)\,(1 - tr_{PPR}) + TC_0 + (TC_n - TC_0)\,(1 - tr_{PPR})\]

\[=\,V_0\,(1 + tcp_{PPR})\,(1 + r)^n\,(1 - cr_{PPR})^n\,(1 - tr_{PPR}) + V_0\,(1 + tcp_{PPR})\,(tr_{PPR})\]

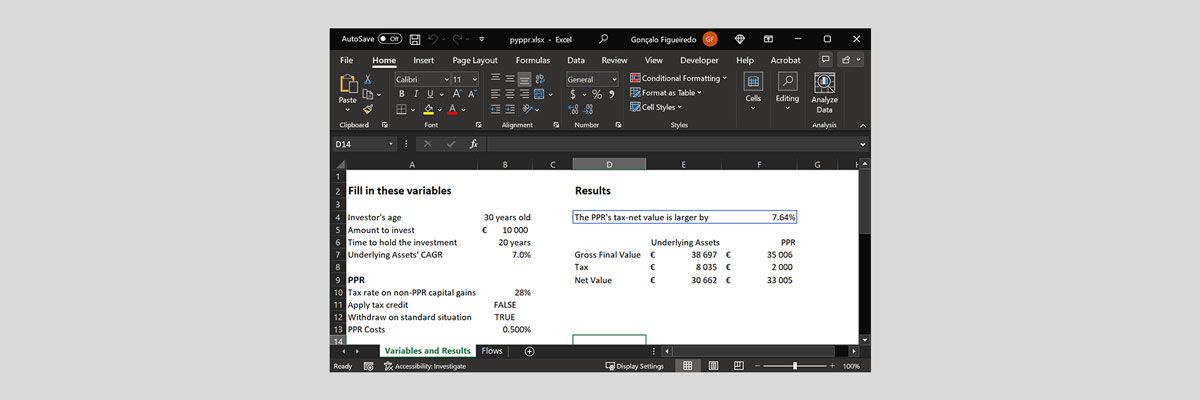
Supporting Excel#

Download the Excel we used to confirm the math above.